By Mayank Kumar Singh, Senior Engineer at Sony Research India
13th April 2023
In this blog, Mayank Kumar Singh encapsulates the paper titled ‘Hierarchical Diffusion Models for Singing Voice Neural Vocoder’ co-authored by Naoya Takahashi and Yuki Mitsufuji which has been accepted at the International Conference on Acoustics, Speech, and Signal Processing 2023 (ICASSP) in Rhodes Island, Greece between 04th-10th June 2023.
Neural vocoders generate a waveform from acoustic features using neural networks and have become essential components for many speech processing tasks such as text-to-speech, voice conversion, and speech enhancement, as they often operate in acoustic feature domains for the efficient modelling of speech signals.
For example, in the paper “Robust One-shot Singing Voice Conversion” and “Nonparallel Emotional Voice Conversion for unseen speaker-emotion pairs using dual domain adversarial network & Virtual Domain Pairing”, voice conversion is applied in the Mel-spectrogram domain and a neural vocoder finally converts the spectrogram to the waveform domain as illustrated in Figure 1.
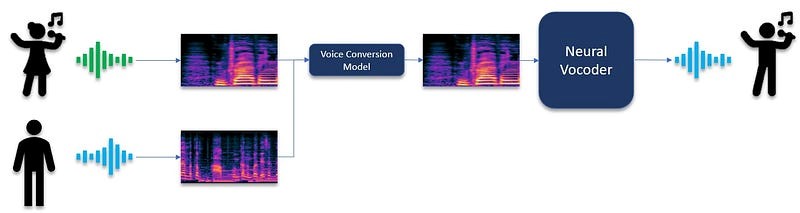
Figure 1: Use of Neural Vocoders in voice conversion algorithms
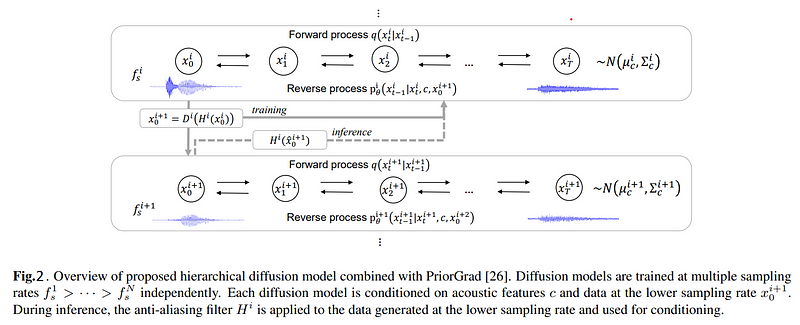
Figure 2: Hierarchical Prior Grad Proposed Method Overview
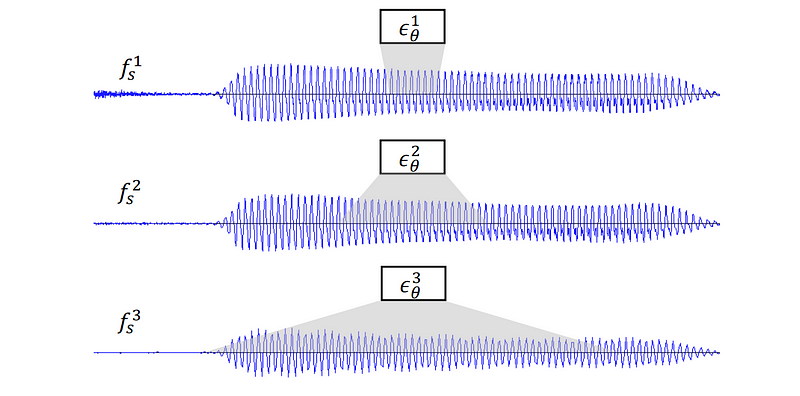
Figure 3: Receptive field at different sampling rates. The same architecture covers a longer time period at lower sampling rates.
We use PriorGrad as a baseline model for our proposed method. Although PriorGrad shows promising results on speech data, we found that the quality is unsatisfactory when it is applied to a singing voice, possibly due to the wider variety in pitch, loudness, and musical expressions such as vibrato and falsetto. To tackle this problem, we propose to improve the diffusion model-based neural vocoders by modelling the singing voice in multiple resolutions. An overview is illustrated in Figure 2. Given multiple sampling rates ƒ¹ₛ > ƒ²ₛ > · · · > ƒⁿₛ, the proposed method learns diffusion models at each sampling rate independently. The reverse processes at each sampling rate fᶦₛ are conditioned on common acoustic features c and the data at the lower sampling rate, except for the model at the lowest sampling rate, which is conditioned only on c. During the training, we use the ground truth data to condition the noise estimation models. Since the noise is linearly added to the original data and the model has direct access to the ground truth lower-sampling rate data, the model can more simply predict the noise for low-frequency components. This enables the model to focus more on the transformation of high-frequency components. At the lowest sampling rate (we use 6 kHz in our experiments), the data become much simpler than that at the original sampling rate, and the model can focus on generating low-frequency components, which is important for accurate pitch recovery of a singing voice. The training algorithm is illustrated in Figure 4.

Figure 4: Training algorithm
During inference, we start by generating the data at the lowest sampling rate and progressively generate the data at the higher sampling rate by using the generated sample at lower sampling rate as the condition. The inference algorithm is illustrated in Figure 5. In practice, we found that directly using the lower sampling rate prediction as the condition often produces noise around the Nyquist frequencies of each sampling rate, as shown in Figure 6(a). This is due to the gap between the training and inference mode; the ground truth data used for training the lower sampling rate model do not contain a signal around the Nyquist frequency owing to the anti-aliasing filter and the model can learn to directly use the signal up to the Nyquist frequency, while the generated sample used for inference may contain some signal around there due to the imperfect predictions and contaminate the prediction at a higher sampling rate. To address this problem, we propose to apply the anti-aliasing filter to the generated lower sampling-rate signal to condition the noise prediction model, as shown in Figure 6(b).

Figure 5: Inference algorithm

Figure 6: Anti-aliasing filter effect in the case of N = 2, ƒ1s =
24000, ƒ2s = 6000.
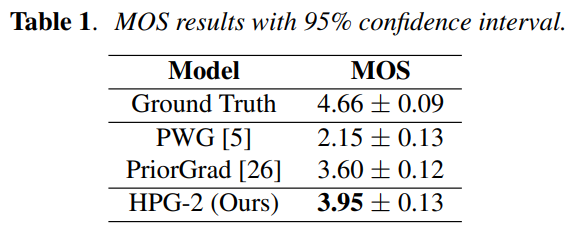
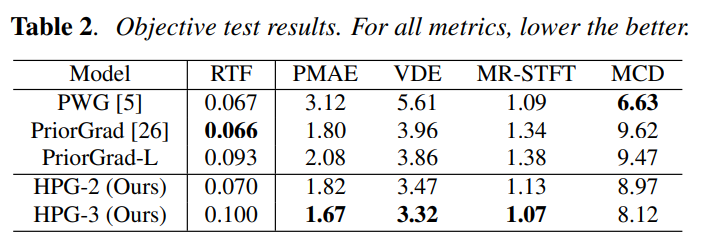
We conducted objective as well as subjective evaluation to evaluate our model against the baseline Parallel WaveGAN and PriorGrad models. For the objective test, we calculate the voice/un-voice detection error (VDE), Multi-Resolution Shot Time Fourier Transform loss (MR-STFT), Mean Cepstral Distortion (MCD), Real-Time Factor (RTF) and Pitch Mean Absolute Error (PMAE). For the subjective test, we asked 20 human evaluators to rate the generated samples using a five-point scale (Mean Opinion Score: MOS). The results are shown in Table 1 and Table 2.
Audio Samples are demonstrated on the website at https://t-naoya.github.io/hdm/
We proposed a hierarchical diffusion model for singing voice neural vocoders. The proposed method learns diffusion models in different sampling rates independently while conditioning the model with data at the lower sampling rate. During the inference, the model progressively generates a signal while taking care of the anti-aliasing filter. Our experimental results show that the proposed method applied to PriorGrad outperforms PriorGrad and Parallel WaveGAN at similar computational costs. Although we focus on singing voices in this work, the proposed method is applicable to any type of audio. Evaluating the proposed method on different types of audio such as speech, music, and environmental sounds will be our future work.
To access/download the paper ‘HIERARCHICAL DIFFUSION MODELS FOR SINGING VOICE NEURAL VOCODER’, click here: https://arxiv.org/pdf/2210.07508.pdf
To know more about Sony Research India’s Research Publications, visit the ‘Publications’ section on our ‘Open Innovation’s page: